2016年度発展プログラミング演習練習問題中級

1. 逆ポーランド記法の計算機

問題

逆ポーランド記法での計算機を作成しましょう．逆ポーランド記法とは，後置記法とも呼ばれます．中置記法と呼ばれる通常の記法は，1 + 2 ですが，これを逆ポーランド記法で書くと，1 2 +となります．コマンドライン引数で，このような計算式を受け取り，計算結果を出力するプログラムを書いてください．

まずは，１桁の数値の四則演算のみを受け入れる計算機を作成しましょう．また数値は全て Integer で扱ってください．

クラス名は，ReversePolishNotationCalculatorとしましょう．

実行例

$ java ReversePolishNotationCalculator "1 2 +"
3 (1 2 +)
$ java ReversePolishNotationCalculator "1 2 +" "3 4 +"
3 (1 2 +)
7 (3 4 +)
$ java ReversePolishNotationCalculator "1 2 + 9 6 - *"
9 (1 2 + 9 6 - *)

引数で受け取った文字列を逆ポーランド記法で書かれた数式と捉えて，計算してください．計算結果を出力後，同じ行に計算の元となった数式を１行で出力してください．

複数の計算式が指定された場合，一つの数式を１行で出力するようにしてください．

ヒント

与えられた文字列をスペースで区切って，最初から順に処理していきましょう．今，見ている文字列（スペースを含まない）が数値の場合は，Listに追加しましょう．数値でなく演算子の場合は，Listの後ろから2つの数値を取り出し，演算子に従った処理を行い，計算結果をListに追加しましょう．

上記の繰り返しで逆ポーランド記法の計算機は実現できます．上記の処理内容は，実は，スタックそのものです．

2. 迷路の作成．

問題

棒倒し法により迷路を作成してください．棒倒し法とは，次の手順で作成する迷路のことです．

迷路の初期化
1. $n\times m$の迷路を作るとする．$n$, $m$は奇数とする．
2. 壁を作成する．
  - 0行目，$n-1$行目を壁にする．
  - 0桁目，$m-1$桁目を壁にする．
3. すべての偶数行目，偶数桁目に柱を立てる．
4. スタート地点を設定する．端っこの壁をスタート地点とする．
5. ゴール地点を設定する．端の壁のうち，スタート地点とは異なる点をゴールとする．
棒倒し法により迷路を作成する．
1. 柱を起点に，乱数で４方向のいずれかに柱を倒し壁を作成する．柱の部分と倒した先の部分が壁となる．
  - 一番左端の列の柱のみ４方向に倒し，壁を作る．
  - その他の柱は上下右方向のみに倒し，壁を作る（左方向には倒さない）．

クラス名は，MazeBuilderとしましょう．

実行例

$ java MazeBuilder
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
    X     X X X X         X X X       X X
XXX X XXXXX X X X X X X X X X X XXXXXXX X
X X       X     X X X X X         X     X
X X X X XXX XXXXX X X X X XXX XXX X X XXX
X   X X     X         X X X X   X X X X X
XXX X X X XXX X XXX XXX X X X X X X XXX X
X X   X X     X   X       X X X X X     X
X X XXXXXXXXX XXX X X XXX X X XXX X XXXXX
X     X     X   X   X   X X X X     X   X
X XXXXX XXX X X X X X XXXXX X X XXX X X X
X         X X X X X       X X   X X X X X
X X XXX X X X XXX X XXXXXXX X X X X X X X
X X   X X X     X X X X       X X   X X X
XXX XXX XXX XXX X XXX X XXXXXXX X X X X X
X     X X X X X X X   X   X   X   X X   X
X XXX XXX X X X X X X X X X XXX X XXX XXX
X   X   X X       X X   X       X X X   X
X X XXX X X XXX XXX X X X X X X X X X XXX
X X   X       X       X   X X X X        
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

41×21の迷路です．実行するたびに異なる迷路が作成されます．

Table型を利用する場合は，Table型の変数に対して， printメソッドを呼び出せば左のような実行結果になります．

ヒント

Table<String> table = new Table<String>(41, 21);
table.set("X", 0, 1);
String item = table.get(0, 1);

迷路を作成するには，二次元配列が必要になります．二次元配列の使い方がわからない人は， Table.javaを利用してください． Table.javaは左の１行目のように，どんな型を入れるTableにするか，何行×何桁のTableにするかを決めます．そして，値を設定するには，setメソッドに値とx, yのインデックスを指定します．値を取得するときは，x, yのインデックスを指定して取得します．

参考資料

乱数の求め方

3. ２つの文字列間の類似度・距離

問題

概要

コマンドライン引数で与えらえた2つの文字列の類似度を次の5つの方法で求めてください．

Simpson係数
Jaccard係数
Dice係数
コサイン類似度
編集距離（Levenshtein距離）

クラス名は，StringSimilarityとしてください．

Simpson係数（Simpson Index）

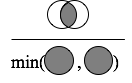2つの集合があったとき，右図のように，両方の集合の要素数のうち短い方で積集合を割ったものが Simpson係数です．

文字列（String型）は，Character型の集合と考えられます．そのため，2つの文字列それぞれの長さ，積集合を計算できれば，Simpson係数が求められます．

Jaccard係数（Jaccard Index）

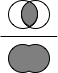2つの集合があったとき，右図のように積集合を和集合で割った値がJaccard係数です．

文字列（String型）は，Character型の集合と考えられます．そのため，2つの文字列の積集合，和集合を計算できれば，Jaccard係数が求められます．

Dice係数（Dice Index）

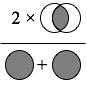2つの集合があったとき，右図のように，積集合の2倍の数を，集合の要素数の和で割ったものが Dice係数です．

文字列（String型）は，Character型の集合と考えられます．そのため，2つの文字列それぞれの長さ，積集合を計算できれば，Dice係数が求められます．

コサイン類似度（Cosine similarity）

2つのベクトルを考え，そのベクトルの成す角のコサインがコサイン類似度です．文字列を文字を要素とするベクトルと考え，2つの文字列から2つのベクトルを構築します．

2つのベクトル $\vec v_1, \vec v_2$があるとき，2つのベクトルのコサインは， $\cos \theta = (\vec v_1 \cdot \vec v_2)/(|\vec v_1||\vec v_2|)$で求められます．文字列から，文字の頻度を計算し，それをベクトルとして扱えば，コサイン類似度が求められます．

"value1"と"value2" の2つの文字列を考えてみましょう． 2つの文字列からそれぞれベクトルを作成して，$\vec v_1 = \{ 1, 1, 1, 1, 1, 1, 0 \}$， $\vec v_2 = \{ 1, 1, 1, 1, 1, 0, 1 \}$とします．ベクトルの各要素は， {'v', 'a', 'l', 'u', 'e', '1', '2'}としています． $\cos \theta$を求める式に当てはめると，$\frac{5}{\sqrt{6}\sqrt{6}}$となり， "value1"と"value2" のコサイン類似度は，0.83333...と計算できます．

編集距離（Levenshtein distance）

編集距離（Levenshtein距離）とは，2つの文字列がどの程度異なっているかを表す距離のことを指します．一方の文字列から，もう一方の文字列に変更するまでに必要な，１文字の挿入，削除，置換の最小手順で距離を定義しています．

例えば，次の手順を行えば，"distance"から "similarity"に変更できます．この場合，8回の手順で変更できたため，編集距離は 8 となります．

"distance"
"sistance"．（1文字目のdをsに置換）
"simtance"．（3文字目のsをmに置換）
"simiance"．（4文字目のtをiに置換）
"similance"．（5文字目にlを追加）
"similarce"．（7文字目のnをrに置換）
"similarie"．（8文字目のcをiに置換）
"similarit"．（9文字目のeをtに置換）
"similarity"．（10文字目にyを追加）

実際に長さ$n$と$m$の文字列$S_n, S_m$間の編集距離を計算するには，$(n+1)(m+1)$の表が必要になります．この表のことを編集グラフ（Edit graph）と呼びます．

表の初期化処理は次の通りです．
- $n=0$の$i$列目に$i$を代入します．
- $m=0$の$j$行目に$j$を代入します．
- 結果として，一番上の行，一番左の列のみに数値が入れられた表が得られます．値は，左（下）になるにつれ1ずつ増えていきます．
表の空いている場所に次のルールに従って値を埋めていきます．
- 注目しているセルの上，左のセルの値に1を足します．($d_1$, $d_2$とします)
- $S_n$の$n$番目の文字と$S_m$の$m$番目の文字を比較します．異なっていればコストを1，同じであれば，コストを0とします．
- 注目しているセルの左上のセルに，先ほど求めたコストを足します（$d_3$とします）
- $d_1$，$d_2$，$d_3$を比べ，一番小さな値を注目しているセルの値として更新します．
- 上記をすべてのセルに対して行います．
すべての値が埋められた表が得られたとき，一番右下の値が編集距離です．

編集グラフの作成表の作成イメージは右図の通りです．まず，0行目，0列目を埋めます．その後，空いているセルを左上から順に埋めていきます．当該セルの値は，上，左，左上の3つのセルの値から求められます．基本的には，上，左，左上のセルの値に1を加算した値を求めます．ただし，それぞれの文字列の対応する文字が一致した場合，左上のセルの値をそのまま利用します（1の加算は行いません）．その上で，3つの数値を比較し，一番小さな値がそのセルの値として表が更新されます．

なお，上のセルの値が選択された場合，文字が追加されるコストを指し，左のセルの値が選択された場合は，文字の削除，左上のセルの値が選択された場合は，文字の置換を意味しています．

       d  i  s  t  a  n  c  e 
    0  1  2  3  4  5  6  7  8 
 s  1  1  2  2  3  4  5  6  7 
 i  2  2  1  2  3  4  5  6  7 
 m  3  3  2  2  3  4  5  6  7 
 i  4  4  3  3  3  4  5  6  7 
 l  5  5  4  4  4  4  5  6  7 
 a  6  6  5  5  5  4  5  6  7 
 r  7  7  6  6  6  5  5  6  7 
 i  8  8  7  7  7  6  6  6  7 
 t  9  9  8  8  7  7  7  7  7 
 y 10 10  9  9  8  8  8  8  8

この説明を何度も読むより，いろいろなパターンで表を作成して，結果を確認する方が理解が深まるでしょう． "distance"と空文字や"a" との比較などパターンを変えて実行してみましょう．

実行例

$ java StringSimilarity distance similarity
simpson(distance, similarity)=0.500000
jaccard(distance, similarity)=0.333333
dice(distance, similarity)=0.500000
cosine(distance, similarity)=0.530330
edit_distance(distance, similarity)=8
$ java StringSimilarity android ipodtouch
simpson(android, ipodtouch)=0.428571
jaccard(android, ipodtouch)=0.272727
dice(android, ipodtouch)=0.428571
cosine(android, ipodtouch)=0.502519
edit_distance(android, ipodtouch)=7

すべての類似度・距離を出力してください．また，計算の元となった文字列も出力してください．

ヒント

List<Character> getList(String item){
    List<Character> list = new ArrayList<Character>();
    for(Integer i = 0; i < item.length(); i++){
        Character c = item.charAt(i);
        if(!list.contains(c)){
            list.add(c);
        }
    }
    return list;
}

左のプログラムで，文字列から，重複なしの文字の集合を取得できます．

参考資料

サカナの描画（基礎プロII 再び）

問題

実行の確認

右図のように，サカナが壁に跳ね返りながら泳ぐプログラム FishDrawer.javaがあります．取得して実行し，動きとプログラムを見比べて，内容を理解してください．なお，実行にはEZ.javaが必要です． FishDrawer.javaと同じディレクトリに置いてください．

EZ Graphicsは，ハワイ大学マノア校のAdvanced Visualization and Applications研究室 Dylan Kobayashi によって開発されたソフトウェアです． 1つのファイルを同じディレクトリに置くことで図形の描画が容易に扱えるようになります．この授業向けに少し修正していますので，公式サイトからのダウンロードではなく， EZ.javaを利用してください．

なお，runメソッドとmainメソッドに InterruptedExceptionがthrows節で指定されています．指定ミリ秒だけ処理を止める命令であるThread.sleepを呼び出すときには， InterruptedExceptionが投げられる恐れがあるので，指定しなければいけません．

行うべきこと．

このプログラムは，右に進むときでもサカナが左向きになっています．これを修正し，サカナが正しい方向を向いて進むようにしてください（横の壁に当たって，進行方向が逆転したら，描くサカナを右向き（あるいは左向き）にする）．左向きのサカナを描くメソッドはすでに定義されているので，その内容をもとに，右向きのサカナを描くメソッドを定義しましょう．そして，左右の進行方向に合わせて，どちらのメソッドを呼び出すかを変更しましょう．

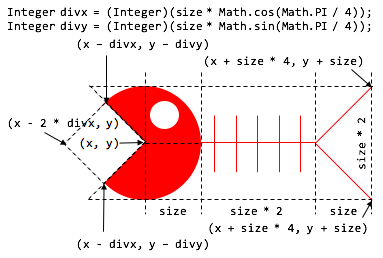なお，サカナの座標は右図の通りです．なお，プログラムのdrawFishメソッド内，EZ.addPolygon メソッドを呼び出しています．この呼び出しが少し複雑ですが， xp，ypへの代入は，菱形の4つの座標を意味しています．最初に円を描いた上に，背景色で菱形を描くことで，口の描画を実現しています．

上記のことができれば，複数のサカナ（4, 5匹）を描画してみましょう．それぞれのサカナの座標を独自の型で管理し，サカナ型をリストで持ちましょう．また，それぞれのサカナで，色も変更してみましょう．

実行例

サカナ行うべきことは以下の通りです．順番に行っていきましょう．

実行の確認から必要なファイルをダウンロードし，実行結果を確認する．
右向きサカナを描画するメソッドを追加する．
複数のサカナを描画するようプログラムを拡張する．それぞれのサカナの座標を管理するため，独自の型を定義する．
それぞれのサカナの色を変更してみましょう．

2016年度発展プログラミング演習練習問題中級

目次

1. 逆ポーランド記法の計算機

問題

実行例

ヒント

挑戦課題

参考資料

2. 迷路の作成．

問題

実行例

ヒント

参考資料

3. ２つの文字列間の類似度・距離

問題

概要

Simpson係数（Simpson Index）

Jaccard係数（Jaccard Index）

Dice係数（Dice Index）

コサイン類似度（Cosine similarity）

編集距離（Levenshtein distance）

実行例

ヒント

参考資料

サカナの描画（基礎プロII 再び）

問題

実行の確認

行うべきこと．

実行例

参考資料