ニュートン法による平方根の計算
アルゴリズム
平方根は Math.sqrtメソッドの呼び出しで求められると述べました.
ここでは,Math.sqrtを使わず,ニュートン法を用いて平方根を計算してみましょう.
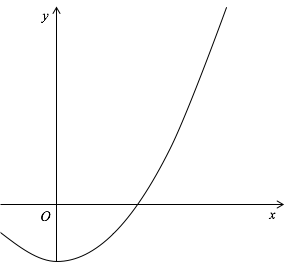
ニュートン法は,関数$f(x)$が与えられた時,その導関数$f’(x)$を用いて,$f(x) = 0$となる解$x$を数値的に求める方法です. $f(x)=x^2 - 2$とすると,$f(x)=0$の解は$x=\sqrt{2}$ ($x > 0$のとき)です. このように,$f(x)=x^2 - n$の解$x=\sqrt{n} (x > 0)$をニュートン法で求めることで,平方根を計算します.
ニュートン法のアルゴリズムは次の通りです.
- 適当な出発点$x_0$から始まります.
- $f(x_0)$の時の$y$座標の値を計算し,$(x_0, y_0)$を求めます.
- $y_0$の絶対値が閾値(threshold; $0.00001$程度)より小さければ,$x_0$が平方根の値となります.
- $(x_0, y_0)$における$f(x)$の接線の式$l_0$を求めます.
- $l_0$と$x$軸との交点座標を求めます.この交点を$x_1$とし,手順の最初に戻ります(今までの$x_0$を$x_1$に置き換えて処理を進めてください).
絶対値
絶対値は,Math.absメソッドを利用して求められます.
Double value = -10.5;
Double positiveValue = Math.abs(value);
// => 10.5 が代入される.
例題
実際にニュートン法のプログラムを書いてみましょう.
public class SquareRoot{
void run(String[] args){
for(Integer i = 0; i < args.length; i++){
Double value = new Double(args[i]);
Double result = calculate(value);
System.out.printf("sqrt(%f) = %f (%f)%n",
value, result, Math.sqrt(value));
}
}
Double calculate(Double n){
Double threshold = 0.00001;
Double xValue = 10.0; // 初期値 x0
Double yValue = function(n, xValue);
// ここにニュートン法のプログラムを書きましょう.
// |yValue| < threshold ならばループを抜ける.
// (yValue の絶対値が閾値(threshold)よりも小さい)
while(...){
// xValue における放物線f(x)傾きを求める.
// 傾き(slant)は 2 * xValue で求められる.
// f'(x)=2x であるため.
// 次は,接線が y 軸と交わる切片 b を求める(y = a x + b).
// (xValue, yValue) を通り 傾き a は先ほど求めた.
// そのため,b = yValue - (slant * xValue) で求める.
// 次に,接線が x 軸と交わるときの xValue の値を求める.
// yValue に 放物線の y の値(xValueを元に求める)を代入する.
}
return xValue;
}
// x^2 - n を計算するメソッド.
Double function(Double n, Double x){
return x * x - n;
}
}
出力例
$ java SquareRoot 2 3 4 5 6
sqrt(2.000000) = 1.414214 (1.414214)
sqrt(3.000000) = 1.732051 (1.732051)
sqrt(4.000000) = 2.000000 (2.000000)
sqrt(5.000000) = 2.236070 (2.236068)
sqrt(6.000000) = 2.449490 (2.449490)