練習問題

1. 与えられた文字列のソート

以下の条件を満たすように，コマンドライン引数 で与えられた複数の文字列をソートして出力するプログラムを作成してください （ソートアルゴリズムを自分で書く必要はありません）．

  • 配列を画面に出力するためのprintArrayを実装してください．
    • printArrayで接頭辞を出力できるようにしてください．
  • ソートの前後で，printArrayメソッドを使って配列の要素を出力してください．
  • クラス名は，ArgsSorterとしてください．

ソートは Arraysに対して，sortメソッドを呼び出すと渡した配列の要素がソートされます． ただし，Arraysを利用する場合は，import java.util.Arrays;という一文が クラス宣言の前に必要です．

public class ArgsSorter{
  void run(String[] args){
    // ここで，printArray を呼び出し，"before"の一行を出力する．
    // argsの内容をソートするため，Arrays.sortメソッドを呼び出す．
    Arrays.sort(args); // <= args がソート済みになる．
    // ここで，printArray を呼び出し，"after"の一行を出力する．
  }
  // printArrayメソッドをここに書く．
  // mainメソッドは省略．
}

実行例

$ java ArgsSorter one two three four five six
before: one, two, three, four, five, six, 
after: five, four, one, six, three, two, 
$ java ArgsSorter time flies like an arrow
before: time, flies, like, an, arrow, 
after: an, arrow, flies, like, time, 
$ java ArgsSorter 2016 10 6
before: 2016, 10, 6, 
after: 10, 2016, 6,

このように，アルファベット順にソートされていることが確認できます． 最後の例は，間違いではありません．"2016"，"10"，"6"という文字列でソートしている，つまり， １桁目の文字（"2", "1", "6"）でソートしているので，この順で正しいです．

2. 学生証番号の正当性を検証するプログラム

本学の学生証番号（６桁）は，各桁を足し合わせると，10の倍数となるようになっています． コマンドライン引数で与えられた学生証番号が正しいものであるかを判定するプログラムStudentIdValidatorを作成してください． 正しい学生証番号であれば，与えられた学生証番号と共に，valid，正しくない学生証番号であれば，invalid， 与えられた文字列が６桁の学生証番号でなければ，not student idと出力してください．

  • String型のIdを受け取るvalidateメソッドを定義してください．
  • Integer型のIdを受け取るvalidateIdメソッドを定義してください．

それぞれのメソッドの処理は次の通りです。 この処理通りにしなければいけないわけではありませんが、 このような処理にすると各メソッドの役割がわかりやすいと思います。

  • runメソッド
    • 引数で受け取った String型配列の各要素を順にvalidateメソッドに渡す。
  • validateメソッド
    • 引数で受け取ったString型の値の長さを確認する。
      • 6桁の学生証番号でなければ、not student idと出力して終了する。
    • 学生証番号であれば、String型をInteger型に変換する。
    • 変換後のInteger型の変数を validateIdメソッドに渡す。
  • validateIdメソッド
    • 引数で受け取ったInteger型変数の正当性を確認する。

ヒント

文字列の長さを取得するには，String型の変数に対して，length()メソッドを呼び出してください．

実行例

$ java StudentIdValidator 024509
024509: valid
$ java StudentIdValidator 123456
123456: invalid
$ java StudentIdValidator 123455 123456
123455: valid
123456: invalid
$ java StudentIdValidator 123509 244409 1024509
123509: valid
244409: invalid
1024509: not student id

3. 二次方程式の解

2次方程式の解を解の公式を用いて求めるプログラム作成してください． その際，実数解，重解，虚数解を区別して出力するようにしましょう． ただし，以下の条件を満たしてください．

  • クラス名は，QuadraticEquationとすること．
  • run，main以外に，少なくとも，判別式$D$の値を求めるdiscriminantメソッドを作成すること．
  • $ax^2+bx+c$の$a$，$b$，$c$はコマンドライン引数から受け取ること．
  • $a$, $b$, $c$ は Double型の値が与えられるものとする．

なお，解の公式は$\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$，判別式$D=b^2 -4ac$が正の場合は実数解，0の場合は重解，負の場合は虚数解です．

String型からDouble型への変換

文字列からDouble型に変換するには，Double.valueOf(stringValue) を利用する．

// Double value = "3.141592";
    // => 文字列は Double 型にそのまま代入できない．
Double value = Double.valueOf("3.141592");
    // => 文字列の "3.141592" を Double型に変換して代入する．

平方根

平方根は，次のコードで求められます．

Integer two = 2;
Double sqrtOfTwo = Math.sqrt(two); // => 1.41421356...

ヒント

  • Double型の数値を printf で出力するときは，%lfではなく，%fもしくは%gで出力しましょう．
    • %f は実数型の数値（Double，Float）が出力できます．
    • %g も実数型の数値ですが，最適表示となります．
  • NaNが出力された場合，0除算，もしくは Math.sqrt に負の値で計算しようとしています．
    • NaN は Not a Number の略です．
  • 虚数解の場合，実部と虚数部は別々に計算しましょう．
    • 実部は，$-\frac{b}{2a}$，虚数部は $\pm \frac{\sqrt{-D}}{2a} i$ のように計算しましょう．
      • 判別式$D$に $-1$ を掛けているのは，平方根を求めるメソッド（Math.sqrt）に負数を渡すと結果がNaNになるためです．

実行例

$ java QuadraticEquation 1 -4 4
answer = 2.000000
$ java QuadraticEquation 1 -4 8
answer = 2.000000 + 2.000000 i, 2.000000 - 2.000000 i
$ java QuadraticEquation 1 0 -4
answer = 2.00000, -2.00000

4. モンテカルロ法による$\pi$の計算

モンテカルロ法により，$\pi$を計算しましょう． モンテカルロ法とは，乱数を用いて統計計算を行う方法です． ここでは，$\pi$を求めます．次のアルゴリズムに従って実装してください．

  1. 0.0〜1.0の乱数を2つ取得し，$x, y$とします．
  2. 原点と$(x, y)$の距離を計算します．距離は，$\sqrt{x^2+y^2}$で求められます．
  3. 計算した距離が1よりも小さい場合，ヒットしたとみなします
    • 距離が1以下の場合，点は円の内側に存在します（ヒットした）．
    • 距離が1よりも大きな場合，点は円の外側に存在します．
  4. 1〜3を規定回数繰り返します．
  5. ヒットした回数の割合を計算します．
  6. この割合が$\frac{\pi}{4}$になるので，4を掛け$\pi$を計算します．

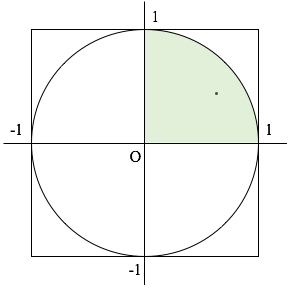
下図のように半径1の円の第１象限に注目します． 0.0から1.0の乱数を2つ取得して，$x, y$とします． 下図の点が得られた乱数値から求められた座標とします．

求められた座標と原点との距離を計算します．距離は，$\sqrt{x^2+y^2}$で求められます． この距離が1よりも小さい場合，円の内側に存在するため，ヒットしたものとします（１回目のクリックの時の画像）．

一方，円の外側にある場合は，ヒットしないものとします（次のクリックの時の画像）． これを規定回数（デフォルトは1000回とします．）繰り返してください． このとき，ヒットした確率は $\frac{\pi}{4}$に近付いていくため， ヒットした確率に 4をかけると$\pi$の近似値が得られます．

クラス名は，MonteCarloPiとします． 引数に値が指定された場合，その値だけ繰り返してください． 値が何も指定されない場合は，1,000回の繰り返しとします．

実行例

計算結果は必ずしもこの通りではありません．

$ java MonteCarloPi
pi = 3.10800
$ java MonteCarloPi
pi = 3.17200
$ java MonteCarloPi 10000
pi = 3.13916
$ java MonteCarloPi 100000
pi = 3.14776
$ java MonteCarloPi 1000000
pi = 3.14127
$ java MonteCarloPi 10000000
pi = 3.14229

5. 台形公式による積分計算を利用した$\pi$の計算

台形公式を用いて$\pi$を計算してください． まず，半径1の円を表す式$x^2＋y^2＝1$を考えましょう． 式を変形すると，$y=\sqrt{1−x^2}$となります． これの$0\leq x \leq 1$の範囲を考えます．

下図のように，この式で描かれるグラフに内接するいくつかの台形を考えます． 下図を１度クリックすると，2つの台形（1つは三角形のように見えますが，上底（右側の高さ）が0に近い台形と考えてください）があり， 横幅は$x_i−x_{i−1}$，高さは$h_{i−1}, h_i$です（$h_{i−1}\ge h_i$）． このとき，一つの台形の面積は，$\frac{(x_i−x_{i−1})\times(h_{i−1}+h_i)}{2}$です． 高さを求めるには，$y=\sqrt{1−x^2}$にその時の$x_i$の値を代入することで求められます．

これをすべての台形について求めます．そして，求めたすべての台形の面積を足し合わせると， $\frac{\pi}{4}$の近似値が得られます． 得られた値に4を掛けると$\pi$が得られます． なお，すべての$i$において，横幅の間隔（$x_i − x_{i−1}$）は同じ値（等間隔）です．

さらに，横幅により狭い値を指定することで，値を$\pi$に近づけられるようになります． さて，この方法で，$\pi$を求めるプログラムを作成しましょう． クラス名は， TrapezoidalRulePiとします． 作成する際に，コマンドライン引数で台形の横幅を指定できるようにしてください． もし，コマンドライン引数で値が指定されなければ，0.001が指定されたものとしてください．

実行例

計算結果は必ずしもこの通りでなくても構いません．

$ java TrapezoidalRulePi 0.01
pi = 3.1375956845831103
$ java TrapezoidalRulePi 
pi = 3.141591477698228
$ java TrapezoidalRulePi 0.001
pi = 3.1414660465553967
$ java TrapezoidalRulePi 0.0000001
pi = 3.141592654152668