2017年度 春学期 発展プログラミング演習

2017-05-11 第５回目 数値計算

本日のテーマ

数値計算

ニュートン法による平方根の計算

平方根は Math.sqrtメソッド呼び出しで求められると述べました． ここでは，Math.sqrtを使わず，ニュートン法を用いて平方根を計算してみましょう．

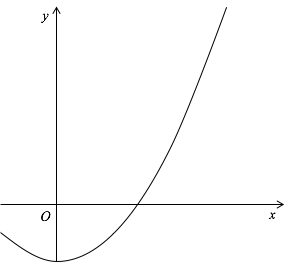
ニュートン法は，関数$f(x)$が与えられた時，その導関数$f’(x)$を用いて，$f(x) = 0$となる解$x$を数値的に求める方法です． $f(x)=x^2 - 2$とすると，$f(x)=$0の解は$x=\sqrt{2}$ ($x > 0$のとき)です． このように，$f(x)=x^2 - n$の解$x=\sqrt{n} (x > 0)$をニュートン法で求めることで，平方根を計算します．

ニュートン法のアルゴリズムは次の通りです．

絶対値は，Math.absメソッドを利用して求められます．

Double value = -10.5;
Double positiveValue = Math.abs(value); // => 10.5 が代入される．

例題

実際にニュートン法のプログラムを書いてみましょう．

public class SquareRoot{
     void run(String[] args){
         for(Integer i = 0; i < args.length; i++){
             Double value = new Double(args[i]);
             Double result = calculate(value);
             System.out.printf("sqrt(%f) = %f (%f)%n", 
                     value, result, Math.sqrt(value));
         }
     }
     Double calculate(Double n){
         Double threshold = 0.00001;

         Double xValue = 10.0; // 初期値 x0
         Double yValue = function(n, xValue);
         // ここにニュートン法のプログラムを書きましょう．

         // yValue の絶対値が閾値（threshold）よりも小さければループを抜ける．
         while(...){
             // xValue における放物線f(x)傾きを求める．傾き slant は
             //     2 * xValue で求められる．f'(x)=2x であるため．
             // 接線は (xValue, yValue) を通り，傾きも求められた．
             // 次は，接線が y 軸と交わる切片 b を求めます（y = a x + b）．

             // 次に，接線が x 軸と交わるときの xValue の値を求めましょう．

             // yValue に 放物線の y の値（xValueを元に求める）を代入しましょう．
         }

         return xValue;
     }
     // x^2 - n を計算するメソッド．
     Double function(Double n, Double x){
         return x * x - n;
     }
}

出力例

$ java SquareRoot 2 3 4 5 6
sqrt(2.000000) = 1.414214 (1.414214)
sqrt(3.000000) = 1.732051 (1.732051)
sqrt(4.000000) = 2.000000 (2.000000)
sqrt(5.000000) = 2.236070 (2.236068)
sqrt(6.000000) = 2.449490 (2.449490)

任意桁の計算

Java言語の IntegerやDouble型は表せる桁数が決まっています．Integerは 32ビット，Longでも64ビットであるため，それぞれ，$-2^{31}〜2^{31} - 1$，$-2^{63}〜2^{63} - 1$ までの値までしか扱えません．

Javaでは任意桁の計算が行える型が存在します．任意桁の整数を表すBigIntegerと任意桁の実数を表すBigDecimalです． これらを扱ってみましょう．

BigInteger

任意桁の整数を表す型です．BigIntegerを利用するときは，import java.math.BigInteger; というimport 文が必要です．BigInteger型の実体を作成するときは，new BigInteger("表したい数") のように数値を文字列で指定してください． この型を扱うとき，通常の四則演算が使えない点に注意してください．

BigInteger value1 = new BigInteger("10");
BigInteger value2 = new BigInteger("20");
BigInteger value3 = value1.add(value2);
// BigInteger value4 = value1 + value2; // => コンパイルエラー．

上記のように，足し算は addというメソッド呼び出しで実現します． 以下に対応を掲載します．どれも BigInteger型の変数b1とb2を使って計算しているものとします．

なお，BigDecimalも基本的にはBigIntegerと同じです． メソッド呼び出しで演算を行い，実体を作成するときは，実数を表す文字列を渡せば良いです．

例題 階乗改

第２回目の練習問題 3. 階乗 を改良し，桁あふれを起こさないようにしましょう． 前回作成した階乗のプログラムは，13!を正確に計算できません．これを BigInteger を使って， どんな数値が与えられたとしても計算できるようにしてください． クラス名をBigFactorialとしてください． コマンドライン引数から値を受け取れるようにしましょう． また，コマンドライン引数で受け取る値はInteger型として扱って良いです．

出力例

$ java Factorial 12 # => 前回のプログラム．正しい結果の限界．
12! = 479001600
$ java Factorial 13 # => 前回のプログラム．正しくない結果が出力されている．
13! = 1932053504
$ java BigFactorial 11
11! = 39916800
$ java BigFactorial 12 13 14 15
12! = 479001600
13! = 6227020800
14! = 87178291200
15! = 1307674368000

複素数 (Complex)

複素数型の定義

複素数型Complexを作成しましょう．フィールドには，Double型のreal，imagを定義してください． また，printメソッドでComplexを出力するようにしましょう．

public class Complex{
    Double real;
    Double imag;
    void print(){
        System.out.printf("%5.2f + %5.2f i", this.real, this.imag);
    }
    void println(){
        this.print();
        System.out.println();
    }
}

上記のように，独自の型にはフィールドとメソッドを同時に定義できます．

複素数型を利用するプログラムの作成

次に，Complexを利用するプログラム ComplexCalculator を作成しましょう．

public class ComplexCalculator{
    void run(){
        Complex c1 = this.createComplex(3.0, 4.0);
        c1.println();
    }
    Complex createComplex(Double realValue, Double imagValue){
        Complex c = new Complex();
        c.real = realValue;
        c.imag = imagValue;
        return c;
    }
    // mainメソッドは省略．
}

上記のrunメソッド内で，Complex型の printメソッドを呼び出しています． このように，メソッドを呼び出すにも，変数を経由して呼び出す必要があります． 一方，変数（フィールド）も変数を経由してアクセスします．createComplexメソッドをみてください． このように，Complex型の変数 c を経由してフィールドにアクセスしています． このように，メソッドもフィールドも，必ず変数を経由してアクセスする必要があります．

例題 absolute

さて，Complex型に Double型を返す absoluteメソッドを追加してください．引数はありません． 複素数の絶対値を返すメソッドです． $z=a+bi$の絶対値$r$は，$r = |z| = \sqrt{a^2 + b^2}$で求められます．

上記が完成すれば，ComplexCalculator で absolute を呼び出し，結果を出力してください．

例題 conjugate

次に，Complex型に Complex型の実体を返す conjugateメソッドを追加してください． 引数はありません．conjugateは共役複素数を意味します．虚部の符号を逆転させたものであり， $z=a+bi$ の共役複素数は，$\bar{z}=a-bi$です．conjugateメソッド内で 新たにComplex型の実体を作成し， 呼び出されたメソッドがもつ複素数の共役複素数として変数に値を代入し，返してください （thisの値を元に，共役複素数を作成し，返してください）．

上記が完成すれば，ComplexCalculator で conjugate を呼び出し，結果を出力してください．

再帰呼び出し（Recursive call）

例題 階乗改2

第２回目の練習問題 3. 階乗を別の書き方をしてみましょう． $n$の階乗は，$n!=n×(n−1)×(n−2)…2×1$ で求められます． この式を漸化式で表すと次の通りです．

\[ n! = \begin{cases} 1 & n=1\\
n \times (n-1)! & n> 1 \end{cases} \]

Javaプログラムでこの漸化式を表してみましょう．

public class Factorial2{
    void run(String[] args){
        for(Integer i = 0; i < args.length; i++){
            Integer number = new Integer(args[i]);
            this.printFactorial(number, this.factorial(number));
        }
    }
    Integer factorial(Integer number){
        if(number == 1){
            return 1;
        }
        return number * this.factorial(number - 1);
    }
    void printFactorial(Integer number, Integer result){
        System.out.printf("%d! = %d%n", number, result);
    }
    // mainメソッドは省略．
}

上記プログラムのfactorialメソッドに注目してください． 引数のnumberの値が1の場合は，返り値として1を返します． そして，numberの値が1以外の場合は，引数として与える数を変更して，factorialメソッドを再度呼び出しています． あるメソッドから，自分自身を呼び出すことを再帰呼び出しと呼びます． 上に示した漸化式で考えると理解が容易でしょう．

再帰呼び出しには，必ず再帰からの脱出口を設ける必要があります． 上の例で言えば，if(number == 1){ return 1; } が脱出口になっています． もし，脱出口が設けられていない，もしくは，設けられていても，適切な条件でなければ再帰から抜け出せず，StackOverflowExceptionが発生します．

また，動作を確認するために，上記プログラムのfactorial メソッドの先頭にSystem.out.printf("factorial(%d)%n", number); という一文を入れて実行してみても良いでしょう．

ページのトップに戻る

練習問題

1. Complexの四則演算

ComplexCalculator に Complexの四則演算を行うメソッドを追加してください．

出力例

$ java ComplexCalculator
absoluate( 5.00 + -6.00 i) =  7.810250 
conjugate( 5.00 + -6.00 i) =  5.00 +  6.00 i
 5.00 + -6.00 i +  3.00 +  2.00 i =  8.00 + -4.00 i
 5.00 + -6.00 i -  3.00 +  2.00 i =  2.00 + -8.00 i
 5.00 + -6.00 i *  3.00 +  2.00 i = 27.00 + -8.00 i
 5.00 + -6.00 i /  3.00 +  2.00 i =  0.23 +  2.15 i

2. GrandTotal改

第１回目の練習問題 4. 総和を求めるを再帰呼び出しを使って計算するプログラムを作成してください． クラス名は，GrandTotal2としてください． また，コマンドライン引数で最大値を与えられるようにしてください．

出力例

$ java GrandTotal2
1から10までの総和は55です．
$ java GrandTotal2 10
1から10までの総和は55です．
$ java GrandTotal2 100
1から100までの総和は5050です．
$ java GrandTotal2 90
1から90までの総和は4095です．

3. Fibonacci数列 改

第２回目の練習問題 5. Fibonacci数列を再帰呼び出しを使って計算してみましょう． Fibonacci数列の$n$項目の値を出力してください． クラス名はFibonacci2としてください．

コマンドライン引数に値が指定されない場合は，10項目が指定されたものとしてください． コマンドライン引数に複数個の数値が与えられた場合，全ての数値に対して結果を出力してください．

出力例

$ java Fibonacci2
55
$ java Fibonacci2 1 2
fibonacci(1) = 1
fibonacci(2) = 1
$ java Fibonacci2 4 10 20
fibonacci(4) = 3
fibonacci(10) = 55
fibonacci(20) = 6765
$ java Fibonacci2 40
fibonacci(40) = 102334155

4. Fibonacci数列 改2

第２回目の練習問題 5. Fibonacci数列を改良し，桁あふれを起こさないようにしてください． 再帰呼び出しではなく，単純な繰り返しでFibonacci数列の$n$項目を求めてください（単純な再帰呼び出しにすると，非常に遅くなるため）． クラス名はBigFibonacciとしてください． Fibonacci数列を Integer型で扱うと，第47項目の計算で桁あふれを起こします．

コマンドライン引数に値が指定されない場合は，10項目が指定されたものとしてください． コマンドライン引数に複数個の数値が与えられた場合，全ての数値に対して結果を出力してください．

出力例

$ java BigFibonacci
fibonacci(10) = 55
$ java BigFibonacci 10 30 46 47 48 49 50
fibonacci(10) = 55
fibonacci(30) = 832040
fibonacci(46) = 1836311903
fibonacci(47) = 2971215073
fibonacci(48) = 4807526976
fibonacci(49) = 7778742049
fibonacci(50) = 12586269025

5. 線形合同法による擬似乱数列

線形合同法（Linear Congruential Generators）を用いて，0〜1の範囲の乱数をコマンドライン引数で指定された数だけ求めてください． コマンドライン引数で何も指定されなかった場合は，10が指定されたものとしてください． クラス名は LinearCongruentialGenerator としてください．

このプログラムも，素数の一覧 と同じように ArrayList<Double>を返すメソッドを作成し， 返されたArrayList<Double>の実体をそのままSystem.out.printlnに渡してください．

線形合同法は，擬似乱数を発生させるアルゴリズムです．以下の漸化式で求めます．

$X_{n+1}=(A\times X_n + B) \mod M$

$A$，$B$，$M$は定数です．$A$は自分の誕生日（月日．3桁もしくは4桁），$B$は1， $M$は65536，$X_0$は自分の年齢としてください． 完成すれば，$A$，$B$，$M$，$X_0$の値を変更して結果がどのように変わるかを確認しましょう． ただし，$A<M$，$B<M$である必要があります．

この問題は，必ずしも再帰呼び出しで作成する必要はありません．

なお，C言語の rand 関数は，この線形合同法を用いて計算されています．

5月10日(水) 11:00 に問題文（$A$，$B$の初期値）を変更しています． 今までの条件であれば，桁あふれを起こすためです． 上記時間以前に作成した人は，$A$，$B$の初期値を修正してください．

この練習問題で作成した乱数の安全性について また，ここで作成した乱数は安全ではありません（未来の出力が容易に予測できます）． そのため，自分自身で作成するプログラムに，このようなアルゴリズムで作成した乱数は使わないようにしてください． 少なくともライブラリとして用意されている乱数を利用してください．

出力例

各自の出力結果は，以下のものと異なる値になります．

$ java LinearCongruentialGenerator
[0.019073486328125, 0.308502197265625, 0.329376220703125, 0.855133056640625, 0.471710205078125, 0.077545166015625, 0.383575439453125, 0.413238525390625, 0.002471923828125, 0.299713134765625]
$ java LinearCongruentialGenerator 2
[0.019073486328125, 0.308502197265625]
$ java LinearCongruentialGenerator 5
[0.019073486328125, 0.308502197265625, 0.329376220703125, 0.855133056640625, 0.471710205078125]

ヒント

乱数値はDouble型で求めますが，$X_{n+1}$の計算式はInteger型で計算する必要があります． つまり，結果を保存するとき，$X_{n+1}$ を $M$で割り，Integer型からDouble型に変換する必要があります．

ArrayList<Double> random(Integer max){
    ArrayList<Double> results = // 結果を格納するリストを作成する．
    Integer a, xn, b, m;
    xn = 20; // X0（自分の年齢）
    // a, b, m にも初期値を代入する．
    // 以下の2行を指定回数繰り返す．
        xn = // 線形合同法の計算式に従い，X_n+1 を求める．
        results.add(1.0 * xn / m); // xnを0.0〜1.0の範囲に変換してリストに追加する．
    return results;
}

6. ニュートン法による立方根の計算

ニュートン法による平方根の計算を参考に立方根を求めてください． クラス名は，CubicRootとします．

出力例

$ java CubicRoot 2 3 4 5 6 8 27
cubic_root(2.000000) = 1.259921
cubic_root(3.000000) = 1.442250
cubic_root(4.000000) = 1.587401
cubic_root(5.000000) = 1.709976
cubic_root(6.000000) = 1.817121
cubic_root(8.000000) = 2.000000
cubic_root(27.000000) = 3.000000

ページのトップに戻る

まとめ