2016-10-27 第６回目グラフィックス

本日のテーマ

グラフィックス
練習問題
まとめ

グラフィックス

EZ.java

本日のプログラムを実行するには EZ.javaが必要です．これから書くプログラムと，同じディレクトリにこのEZ.javaを置いてください．

EZ.java は正式には，EZ Graphics と呼びます．このプログラムは，ハワイ大学マノア校のAdvanced Visualization and Applications研究室 Dylan Kobayashi によって開発されたソフトウェアです． 1つのファイルを同じディレクトリに置くことで図形の描画が容易に扱えるようになります．公式サイトからもダウンロードできますが，この授業向けに少し修正していますので，EZ.javaをダウンロードして利用してください．

楕円の描画

ダウンロードしたら，早速プログラムを書いていきましょう．書き終えたら，コンパイル，実行してみましょう．実行結果を確認できれば，値を変更して再度，コンパイル，実行してみましょう．どこを変更すると，どう変わるのかを確認してください．

import java.awt.Color;
public class DrawOval{
    void run(){
        EZ.initialize(400, 400); // 画面の大きさを決める．
        // 円を描く．(中心座標x, y, 幅，高さ，色，塗りつぶし)
        EZCircle circle1 = EZ.addCircle(100, 100, 200, 200, Color.BLUE, true);
        EZCircle circle2 = EZ.addCircle(200, 200, 200, 200, Color.RED,  false);
    }
    // mainメソッドは省略．
}

DrawOval

座標系

座標は左右方向がx軸，上下方向がy軸になっており，右側がx軸のプラス方向，左端がx軸の0です．また，上下方向では，一番上がy方向の0，下方向がプラスになっていることに注意してください．

例題1. 楕円の描画の変更

円の位置をずらしてください．
円の色を変更してください．
円の大きさを変更してください．

その他の図形の描画

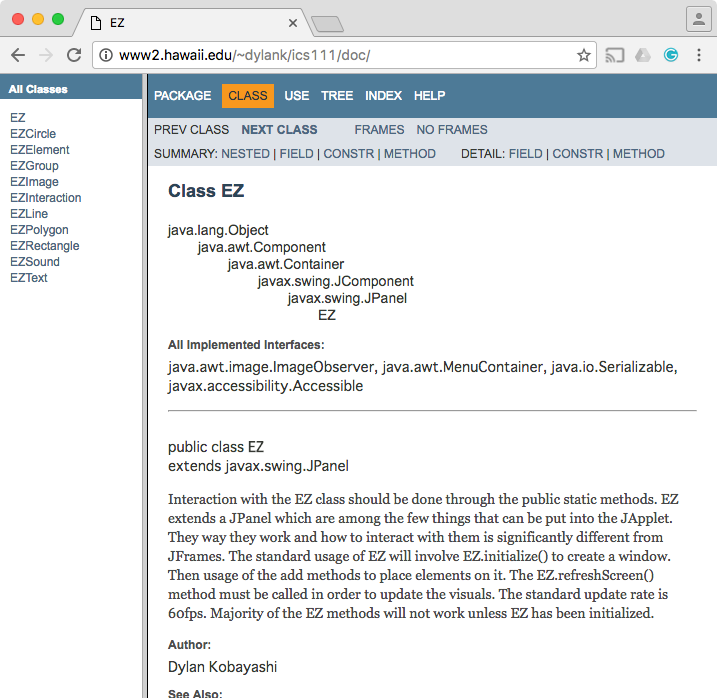
円以外の図形も描いてみましょう．どのようなメソッドを呼び出せば良いかは，EZ Graphicsのドキュメントを読んでみましょう．

http://www2.hawaii.edu/~dylank/ics111/doc/

各ページの左のフレームは，EZ Graphics が持つ型を表しています．右のフレームは，その型が持つ情報を表しています．右のフレームを下にスクロールしていくと，メソッドの一覧が閲覧できます（上の右側の画像）．

この形式のドキュメントを一般に API ドキュメント と呼びます． Javadocコメントで生成されるドキュメントです．

例題2. 楕円以外の図形の描画

では，EZ GraphicsのAPIドキュメントを参照し，楕円以外の図形も描いてみましょう．

まず，DrawOval.javaをコピーしてDrawShapes.javaを作成してください．そして，DrawShapes.javaに追加・変更していってください．なお，DrawShapes.javaのmainメソッドの中身も忘れずに変更しましょう．

例題3. アニメーション

アニメーションは基本的にパラパラ漫画と同じ原理で行います． EZ Graphics では，EZ.addCircleやEZ.addLineなどで追加して返される実体の位置を変更し，EZ.refreshScreen()を呼び出すと画面を更新します．次の例で確認してみましょう．

import java.awt.Color;
public class RoundTrip{
    void run(){
        EZ.initialize(400, 400);
        EZCircle circle = EZ.addCircle(100, 100, 5, 5, Color.BLUE, true);
        this.roundTrip(circle);
    }
    void roundTrip(EZCircle circle){
        Integer vx = 10;
        while(true){ // 無限ループ
            Integer x = circle.getXCenter() + vx;
            circle.translateTo(x, circle.getYCenter());
            if(x >= 400 || x<= 0){
                vx = vx * -1;
            }
            EZ.refreshScreen();
            Thread.sleep(100);
        }
    }
}

Javaで一定時間スリープするのは，Thread.sleepメソッドを利用します． sleepメソッドにスリープする時間（ミリ秒）を渡します．上記の例では，100ミリ秒（0.1秒）スリープしています．

これでコンパイルすると，次のようなコンパイルエラーが発生します．

prog/autumn06/RoundTrip.java:17: エラー: 例外InterruptedExceptionは報告されません。スローするには、捕捉または宣言する必要があります
       Thread.sleep(100);
                    ^
エラー1個

例外機構（Exception Architecture）

例外（Exception）は，近年のプログラミング言語で採用されている実行時エラーの通知機構です．

従来のプログラミング言語，例えば，C言語の場合，fopenで開くファイルが見つからなかった場合，返り値をNULLにすることでエラーを通知していました．この場合，プログラマが責任を持って，返り値の値を確認して，正常か異常かを判断しなければいけませんでした．

一方の例外機構は，異常処理を行うための別の処理経路を作るものです．もし，プログラムの実行途中で何らかの異常が発生した時，それまでに行なっていた処理を中断し，別の処理を行うようにする機構です．

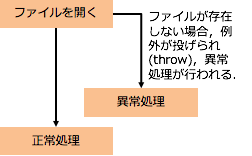
例外が投げられれば，何らかの異常が発生したと判断できるようになります．逆に，例外が投げられなければ，データが変であろうが，正常な処理であると判断できます（もちろん，開発途中で変な場合はバグの可能性はありますが）．

プログラマが明示的に投げる例外も存在しますが，多くの場合，システムが異常を検知し例外を投げます．例えば，ファイルが見つからない場合，スリープ中に割り込みが入った場合などです．そのような例外が発生した時に，どのような対応をするのかをあらかじめ決めておく必要があります．

検査例外と非検査例外

Javaの例外は，検査例外と非検査例外の２つに分類できます．違いは次に挙げる通りです．

検査例外
- 例外が発生した時の処理をプログラム中に明示的に書いておかなければコンパイルエラーになる例外．
- 代表的な検査例外
  - IOException，InterruptedException など．
非検査例外
- 例外が発生した時の処理は書かなくてもコンパイルが通る例外．
- 代表的な非検査例外
  - NullPointerException，ArrayIndexOutOfBoundsException，NumberFormatException
- 非検査例外は，事前にチェックすることで，例外の発生を抑えられます．
  - 非検査例外が投げられた場合は，事前のチェックが不十分であるとも言えます．

InterruptedException の責任転嫁

さて，コンパイルエラーで，InterruptedExceptionが投げられる可能性があると述べられています．この例外は，スリープ中に割り込みが発生した時に発生する例外です．この例外が発生した時の対処法をプログラム中に書いておく必要があります．取れる対処法は２つです．

例外が投げられたら，その場で例外に対応する．
例外が発生する可能性のあるメソッドを呼び出している元に対応を任せる．

どちらがふさわしいかは場合により異なります．ここでは，呼び出し元に対応を任せましょう．以下のような対応になります．

Thread.sleep が例外を発生させた時，Thread.sleep の呼び出し元であるroundTripに対応が任されます．これが例外が投げられた，ということです．
そこで，roundTripの呼び出し元であるrunに対応を任せましょう．
さらに，runでも，呼び出し元であるmainに処理を任せる事にします．
同じく，mainも呼び出し元に対応を任せましょう．
すると，実行環境が対応されなかった例外をスタックトレースという形で出力し，プログラムが終了するようになります．

throws 節

呼び出し元に対応を任せるには，メソッドのシグネチャに throws節を追加します．すなわち，メソッドの宣言部分を以下のように変更してください．

public class RoundTrip{
    void run() throws InterruptedException{
        // ... 省略
        // roundTripで，IntrruptedException が発生する可能性がある．
        this.roundTrip(circle);
    }
    void roundTrip(EZCircle circle) throws InterruptedException{
        // .... 省略
        // ここで，IntrruptedExceptionが発生する可能性がある．
        Thread.sleep(100);
    }
    public static void main(String[] args) throws InterruptedException{
        RoundTrip trip = new RoundTrip();
        // runでIntrruptedExceptionが発生する可能性がある．
        trip.run();
    }
}

このようにプログラムを変更し，コンパイルしてみましょう．今度はコンパイルできたはずです．次のような実行結果となるはずです．

RoundTrip

このように，アニメーションを行うには，スリープが必要です．一方，スリープを行うには，例外への対応が必要になります．今後，ファイルの入出力を扱う時にも例外機構は必要になってきますので，どのような機構であるのか，しっかりと押さえておいてください．

例題4. 鉛直投げ上げ運動のアニメーション

以下の実行結果になるよう，鉛直投げ上げ運動のアニメーションを作成してみましょう．（アニメーションが途中で終わっているので変な挙動のように見えますが，バウンドし続ける動きになっています）

$y$方向の0が一番上，下方向がプラスになっていますので，通常の投げ上げとは方向が逆になっています（上方向に重力がかかっていると思ってください）．必要な式は次の通りです．

時間$t$は0から始まり，0.1ずつ増加するものとする．
- 投げ上げ運動，自由落下運動それぞれに切り替わるとき，$t=0$となる．
重力加速度 $g=9.8$．
投げ上げ運動のとき（下向きに動くとき）
- 初速 $v_0 = 85.0$．
- 初期位置 $y_0 = 0.0$．
- $v<0$となったとき，自由落下運動に切り替わる．
- 現在位置を求める．
  - $y = v_0 t - \frac{1}{2}gt^2$
- その時の速度を求める．
  - $v = v_0 - gt$
自由落下運動のとき（上向きに動くとき）
- 初速 $v_0 = 0.0$
- 初期位置 $y_0 = 368.62$
  - $y_0$ は投げ上げ運動の時の $v=0$となるときであるから，そのときの$t$は次の式で求められる．
    - $0 = v_0 - gt, v_0 = gt, t = \frac{v_0}{g}$，
    - この時の$t$を鉛直投げ上げの位置を求める式に代入し，
      - $y = v_0 \frac{v_0}{g} - \frac{1}{2}g (\frac{v_0}{g})^2 = \frac{2v_0^2 - v_0^2}{2g} = \frac{v_0^2}{2g} = \frac{85.0^2}{2 * 9.8} = 368.62$
- $y < 5$となったとき，投げ上げ運動に切り替わる．
  - 本来の物理世界であれば，跳ね返り係数をかけ，初速が遅くなるが，今回は永遠に繰り返すために，初速は最初に挙げた通りとする．
- 現在位置を求める．
  - $y = y_0 - (v_0 t - \frac{1}{2}gt^2)$．
- その時の速度を求める．
  - $v = v_0 - gt$（投げ上げ運動と同じ）

Bound

ページのトップに戻る

練習問題

1. コッホ曲線（Koch curve）の描画

コッホ曲線は，線分を三等分し，分割点を頂点とした正三角形を描く線です．この作図を無限に繰り返すことで，線分の長さが$\infty$になります．コマンドライン引数でコッホ曲線の $n$ を指定できるようにしましょう．

クラス名は，KochCurveとしてください．コッホ曲線の例を以下に示します．

上記のように，$(x_1, y_1)$と$(x_5, y_5)$が指定された時，$(x_2, y_2)$〜$(x_4, y_4)$を求めましょう．

$l=(\sqrt{(x_5 - x_1)^2 + (y_5 - y_1)^2})/3$
$(x_2, y_2) = (x_1 + l, y_1)$
$(x_3, y_3) = (x_2 + l\cos{\frac{\pi}{3}}, y_2 + l\sin{\frac{\pi}{3}})$
$(x_4, y_4) = (x_1 + 2l, y_1)$

$n=1$までは上記のように計算できますが，$n>2$の場合はこの計算では求められません．次の例を元に考えてみましょう．

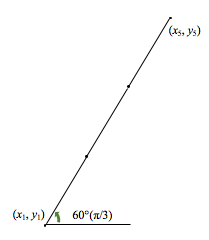
上記のように，$(x_1, y_1)$と$(x_5, y_5)$が指定された時，$(x_2, y_2)$〜$(x_4, y_4)$を求めましょう．元々の傾きを$\theta$として示します．

$l=(\sqrt{(x_5 - x_1)^2 + (y_5 - y_1)^2})/3$
$(x_2, y_2) = (x_1 + l\cos{\theta}, y_1 + l\sin{\theta})$
$(x_3, y_3) = (x_2 + l\cos{(\theta + \frac{\pi}{3})}, y_2 + l\sin{(\theta + \frac{\pi}{3})})$
$(x_4, y_4) = (x_1 + l\cos{(\theta + \frac{\pi}{3} - \frac{2\pi}{3})}, y_1 + l\sin{(\theta + \frac{\pi}{3} - \frac{2\pi}{3})}) = (x_1 + l\cos{(\theta - \frac{\pi}{3})}, y_1 + l\sin{(\theta - \frac{\pi}{3})})$

この計算式で，コッホ曲線を描いてみましょう．再帰呼び出しを利用すると良いでしょう． $(x_2, y_2)，(x_3, y_3)$間の直線を引く時，また，$(x_3, y_3)，(x_4, y_4)$間の直線を引く時にそれぞれを$(x_1, y_1)，(x_5, y_5)$として再帰呼び出しを行えばコッホ曲線を描けるでしょう．

なお，Javaで，sin, cosを計算するには，Math.sin，Math.cosメソッドを利用しましょう．引数にはラジアンの値を渡してください．$\pi$を利用するには，Math.PIという変数を利用してください．すなわち，$\sin \frac{\pi}{3}, \cos \frac{\pi}{3}$をJavaで求めるには，次のようなコードを用いてください．

Double sinValue = Math.sin(Math.PI / 3.0);
Double cosValue = Math.cos(Math.PI / 3.0);

実行例

2. コッホ曲線（Koch curve）のアニメーション描画

コッホ曲線を$n=0$から$n=5$までを3秒程度で更新して描いてみましょう．クラス名は，KochCurveAnimationとしてください．

今まで描画した内容を消したい場合は，EZ.removeAllEZElements() メソッドを呼び出してください．

3. 斜方投射

例題3と例題4を合わせた動きをするボールを描きましょう． $x$軸方向には，例題３を，$y$軸方向には，例題４の動きを設定すれば良いでしょう．

実行例

上記の画像をクリックするとアニメーションが開始され，もう一度クリックすると元の画像に戻ります．

4. アニメーション

EZ Graphics を利用して，自由にアニメーションを描いてください．クラス名は Animation としてください．内容は自由です．